In cardinality sorting, we can no longer use only a sequence of one-digit numbers to enumerate examples. A one-digit sequence is a sort ordering for cardinality sorting.
Here we list the unordered sequence T = [ 2314, 5428, 373, 2222, 17 ]
Sorting principle
As mentioned above, the cardinality sorting does not require comparison and exchange of elements. If you have some algorithms, or a wealth of project experience, I think you may have thought that this might be similar to some "table" or hashing. Counting sorting is the simplest implementation of typing or hashing.
Count sort
The core idea of ​​counting sorting is to build a large enough array of hashArray[], and the array size needs to be guaranteed to include all elements in this array.
Suppose we have an unordered sequence T = [ 2314, 5428, 373, 2222, 17 ]
First initialize the array hashArray[] to an all-zero array. Of course, in Java, this step is not needed, because the default is zero.
When sorting the sequence T, you only need to read the elements in the sequence T in turn, and modify the value in the corresponding position of the element value in the array hashArray[]. There are some circumstance in this sentence. For example, we want to map T[0] to hashArray[], which is hashArray[T[0]] = 1. that is, hashArray[2314] = 1. If there are two identical elements in sequence T, then The value at the corresponding position of the hashArray is 2.
The following figure is a schematic diagram of counting sorting:
(assuming there are unordered sequences: [ 5, 8, 9, 1, 4, 2, 9, 3, 7, 1, 8, 6, 2, 3, 4, 0, 8 ])
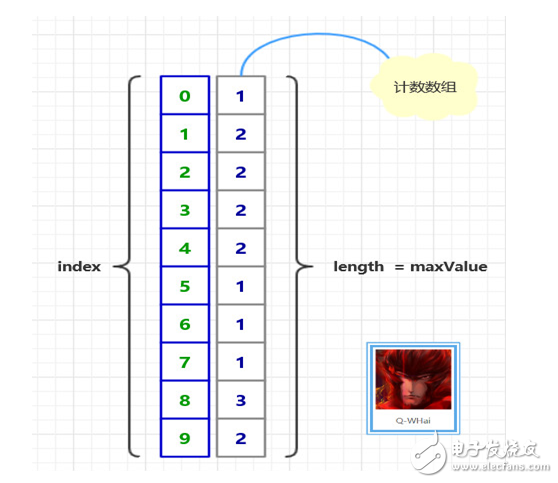
Cardinality sorting schematic
The sorting above is just a guide so that you can learn about cardinal sorting step by step.
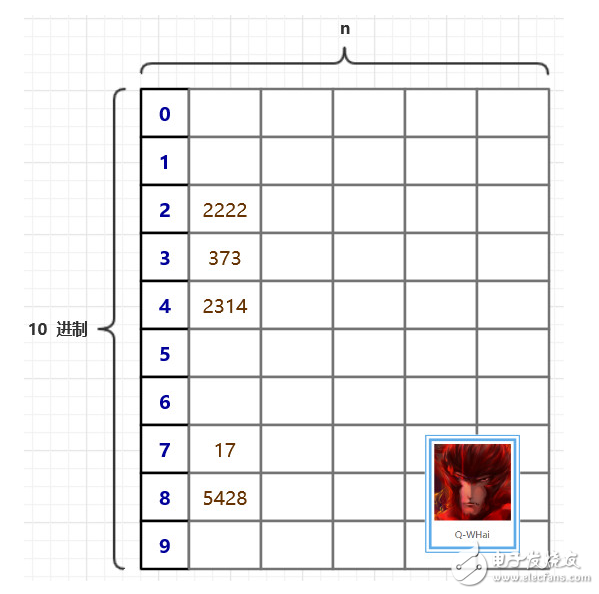
The above picture, perhaps you have already seen it in other blogs. This is a good guide and instructions. In cardinality sorting, we need a large two-dimensional array whose size is (10 * n). 10 means that each of our elements has 10 possibilities, which is a decimal number. In the above figure, we represent this number by the number of digits of each number, so 5428 is filled into the 8th bucket. The next time you fill it, it is filled with ten digits. For example, at 5428, you will choose to represent it by 2.
Algorithm optimization
In the principle of the algorithm, we store these unordered elements as a two-dimensional array of tables. One obvious drawback of using two-dimensional arrays is that the two-dimensional array is too sparse. The utilization of the array is 10%.
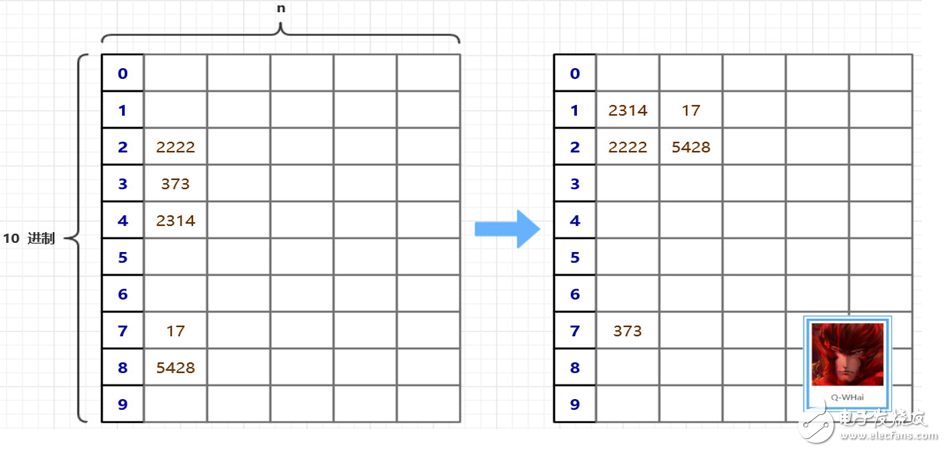
On the way to optimization, we think of a way to compress space, and the time complexity does not deviate too much. That is to design two auxiliary arrays, one is count[] and the other is bucket[]. Count is used to record the index of the last element in a bucket, then calculate the element in the original array to which "bucket" it should belong, and modify the count value of the corresponding position. The highest bit until the maximum number is also added to the bucket, or when all the elements are in the 0th bucket, the cardinality sorting is over.
The optimized schematic is as follows:
Algorithm implementation
Import org.algorithm.array.sort.interf.Sortable;
/**
*
* Cardinal sorting / bucket sorting
*
*
* @author Q-WHai
* @see http://blog.csdn.net/lemon_tree12138
* @version 0.1.1
*/
Public class RadixSort implements Sortable {
@Override
Public int[] sort(int[] array) {
If (array == null) {
Return null;
}
Int maxLength = maxLength(array);
Return sortCore(array, 0, maxLength);
}
Private int[] sortCore(int[] array, int digit, int maxLength) {
If (digit >= maxLength) {
Return array;
}
Final int radix = 10; // base
Int arrayLength = array.length;
Int[] count = new int[radix];
Int[] bucket = new int[arrayLength];
// Count the number of digits in each bucket after assigning the numbers in the array to the bucket
For (int i = 0; i < arrayLength; i++) {
Count[getDigit(array[i], digit)]++;
}
// Convert the number of digits in each bucket into a subscript index of the last digit in each bucket
For (int i = 1; i < radix; i++) {
Count[i] = count[i] + count[i - 1];
}
// Assign the number in the original array to the auxiliary array bucket
For (int i = arrayLength - 1; i >= 0; i--) {
Int number = array[i];
Int d = getDigit(number, digit);
Bucket[count[d] - 1] = number;
Count[d]--;
}
Return sortCore(bucket, digit + 1, maxLength);
}
/*
* The number of digits in the largest number in an array
*
* @param array
* @return
*/
Private int maxLength(int[] array) {
Int maxLength = 0;
Int arrayLength = array.length;
For (int i = 0; i < arrayLength; i++) {
Int currentLength = length(array[i]);
If (maxLength < currentLength) {
maxLength = currentLength;
}
}
Return maxLength;
}
/*
* Calculate how many bits are in a single number
*
* @param number
* @return
*/
Private int length(int number) {
Return String.valueOf(number).length();
}
/*
* Get the number of digits in the d digits of this number
* For example, get 0 digits of 123, the result returns 3
*
* @param x
* @param d
* @return
*/
Private int getDigit(int x, int d) {
Int a[] = { 1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000 };
Return ((x / a[d]) % 10);
}
}
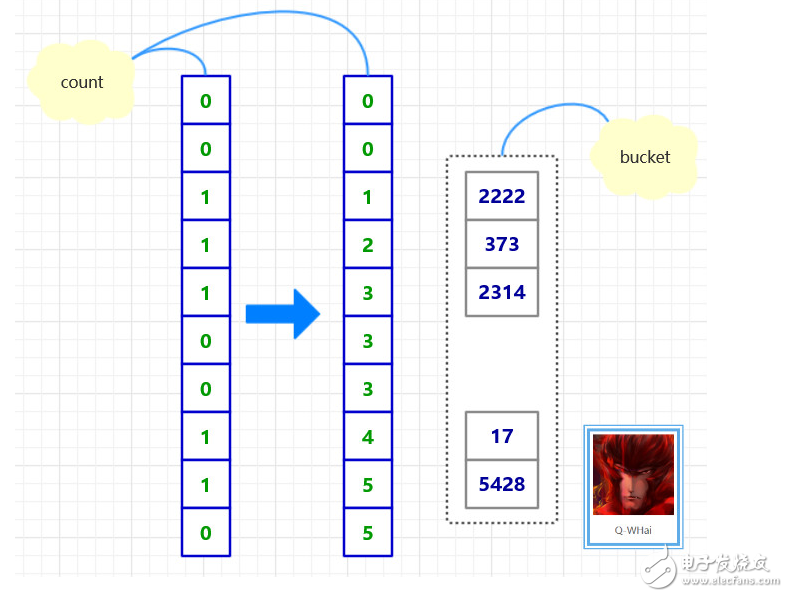
Cardinal sorting process diagram
If our disorder is T = [ 2314, 5428, 373, 2222, 17 ], then the ordering process is as follows.
Cardinal sorting process diagram-1
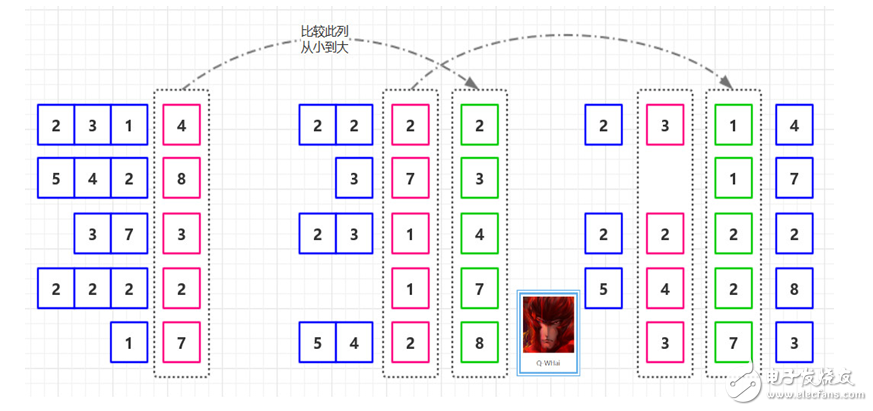
Cardinal sorting process diagram-2
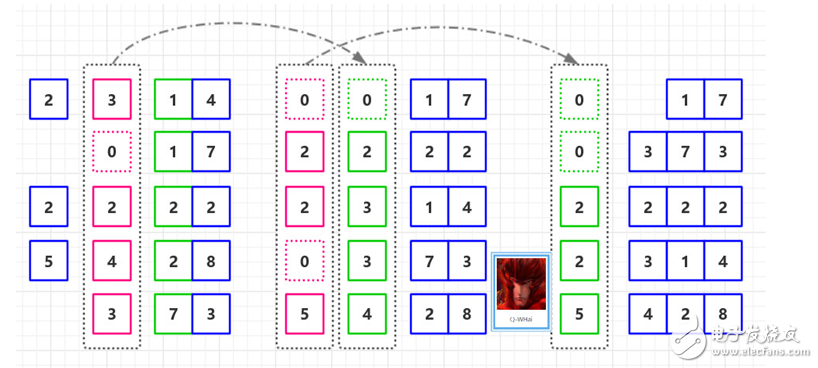
Complexity analysis

Where d is the number of digits, r is the base, and n is the number of the original array.
In the cardinality sorting, since there is no comparison operation, in terms of complexity, the best case and the worst case are consistent in time, both of which are O(d*(n + r)).
SUPBLISS Glitter 5800 Puffs Disposable e cigarette 850mAh Rechargeable Battery 12ml Mesh Coil Vape Pen Case 12 Colors Original RandM
Supbliss Glitter 5800 is a disposable vape device with box design. It contains 12ml 0/2/3/5% nicotine salt e-juice and vape up to 5800 puffs. There are 10 flavors for you to choose. The airflow control let you choose the best spot suit yourself plus it comes with a rechargeable Type-C port at the buttom of the device, which gurantte you finish the last drop of the ejuice in the tank all the time.
Quick Description:
☑ 0% 2% 3% 5% Nicotine Salt
☑ Puffs: 5800
☑ Capacity: 12ml Juice
☑ 10 pcs in a display box, 300pcs master case
☑ 12 flavors available
☑ Mesh Coil
☑ 850mah rechargeable
Flavor List :
1.Blue Razz Ice
2.Strawberry Mango
3.Energy
4.Strawberry Kiwi
5.Sakura Grape
6.Watermelon Ice
7.Lemon Mint
8.Mango Peach
9.Cranberry Grape
10.Kiwi Passion Fruit Guava
11.Red Mojito
12.Cherry Lychee


Supbliss Glitter 5800puffs, 12 flavors available ,Supbliss disposable vape pen
Shenzhen Kester Technology Co., Ltd , https://www.kesterpuff.com