main content:
Why is the negative direction of the gradient the fastest direction of local decline?
When I first came into contact with the concept of gradient descent, when learning machine learning algorithms, many training algorithms used gradient descent, and then the data and teachers also said that they moved toward the opposite direction of the gradient, and the function value dropped the fastest, but When it comes to reasons, many people are unclear. So I sorted out my own understanding and proved this conclusion from the perspective of the direction derivative, let us know that it knows why.
This time from the perspective of optimization to explain:
When we are in a function to be optimized, set to f(x) here, we move at point x and then move along direction v to f(x+v), which shows the movement:
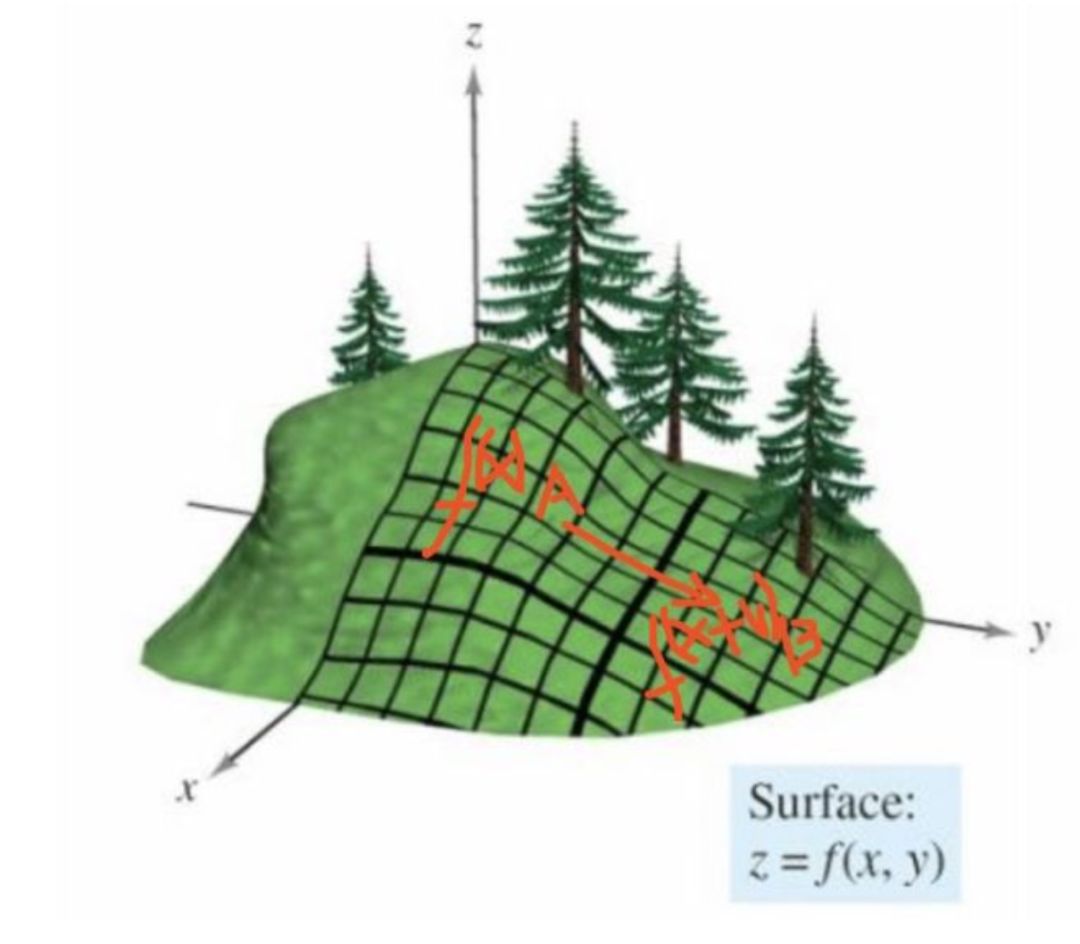
The figure above shows the process of moving from point A to point B. So when is the v direction, is the local drop the fastest?
In the case of a mathematical language, the value of f(x+v)-f(x) is maximized when v is what it is!
Explain below:

Then f(x+v)-f(x)=df(x)v , then we can get: df(x)v is the change of the function value, we should note that df(x) and v are both Vector, df(x)v is the dot product of two vectors, and the vector performs the maximum value of the dot product, that is, when the two are collinear, that is, when the direction of v is the same as the direction of df(x), The dot product value is the largest, and this dot product value also represents the amount of rise from point A to point B. The dot product is described as follows:

And df(x) is the gradient representing the value of the function at x. It is also explained that when the direction of v and the direction of df(x) are the same, the dot product value (change value) is the largest, so that the gradient direction is the direction in which the function locally rises the fastest. It also proves that the negative direction of the gradient is the fastest direction of local decline!
NINGBO LOUD&CLEAR ELECTRONICS CO.,LIMITED , https://www.loudclearaudio.com