Imagine that we want to ride from the University of Berkeley to the Golden Gate Bridge. Although it is only 20 kilometers away, if we are faced with a big problem: you never ride a bicycle! What's worse is that you have just arrived in the Bay Area and are unfamiliar with the road conditions. You only have one map of the city on hand. How can we cycle to see the Golden Gate Bridge? This seemingly complicated task is the problem that robots need to solve with reinforcement learning.
Let us first see how to learn to ride a bike. One way is to learn as much as possible and plan your actions step-by-step to achieve this goal: by reading how to ride a bike, learning related physics, and planning the movement of each muscle during cycling. ...This kind of board-to-appetite approach is OK in the study, but if it is used to study bicycles, it will never reach the Golden Gate Bridge. Learning the correct posture of a bicycle is constantly trying to try and do it wrong. Problems such as learning to ride a bicycle are too complex to achieve through planning.
When you learn to ride, the next step is if you are from Berkeley to the Golden Gate Bridge. You can continue to use trial and error strategies to try various paths to see if the end point is at the Golden Gate Bridge. But the obvious disadvantage of this approach is that we may need a very long time to arrive. For such a simple problem, planning based on existing information is a very effective strategy. It can be completed without too much real-world experience and trial and error. In reinforcement learning, it means a more efficient sampling process.

For some skills, trial and error learning is very effective, but for other plans it is better
Although the above example is simple but it reflects the important characteristics of human intelligence, for certain tasks we choose to use trial and error, and some tasks are based on planning. Different methods also apply to different tasks in reinforcement learning.
However, in the above example, the two methods are not completely independent. In fact, if the method of trial and error is used to summarize the learning process of the bicycle, it is too simple. When we use the trial and error method to learn bicycles, we also use a little planning method. It may be that your plan is not to fall at the beginning, and then you do not fall and ride two meters. Finally, as your technology continues to improve, your goals will become more abstract. For example, if you want to ride to the end of the road, you need to pay more attention to how to plan this goal rather than the details of cycling. It can be seen that this is a process of gradually shifting from no model to model-based strategy. If this strategy can be transplanted into reinforcement learning algorithms, then we can get both good performance (initial phase trial and error methods) and high sampling characteristics (in the later conversion to the use of planning to achieve more abstract goals) Excellent algorithm.
This article mainly introduces the time domain difference model, which is a reinforcement learning algorithm that can smoothly bridge the modelless and model based strategies. The next step is to introduce how model-based algorithms work.
Model-based reinforcement learning algorithm
In the reinforcement study, through the dynamic model, the state transitions from st to st+1 under the action of at, and the goal of the learning is to maximize the sum of the reward functions r(st, a, st+1). The model-based reinforcement learning algorithm assumes that a dynamic model is given in advance. Then we assume that the learning objective of the model is to maximize a series of state reward functions:
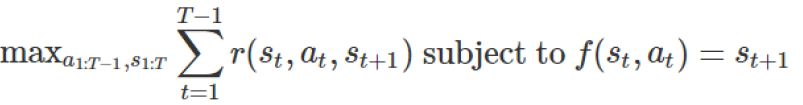
This objective function means that a series of states and behaviors are selected and the reward is maximized while ensuring that the goals are feasible. Feasibility means that every state transition is valid. For example, only st+1 is a feasible state in the following figure. Transfers that are infeasible even though other states have higher reward functions are ineffective.
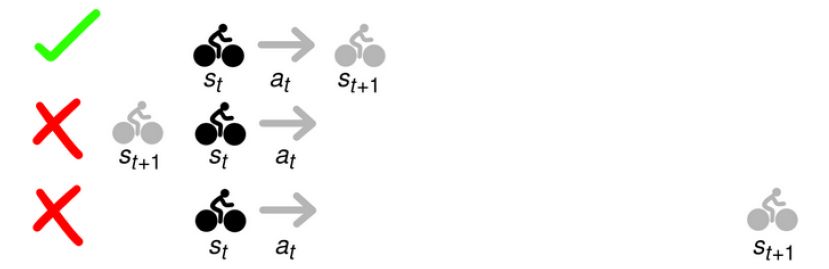
In our riding issue, the optimization problem requires planning a route from Berkeley to the Golden Gate Bridge:
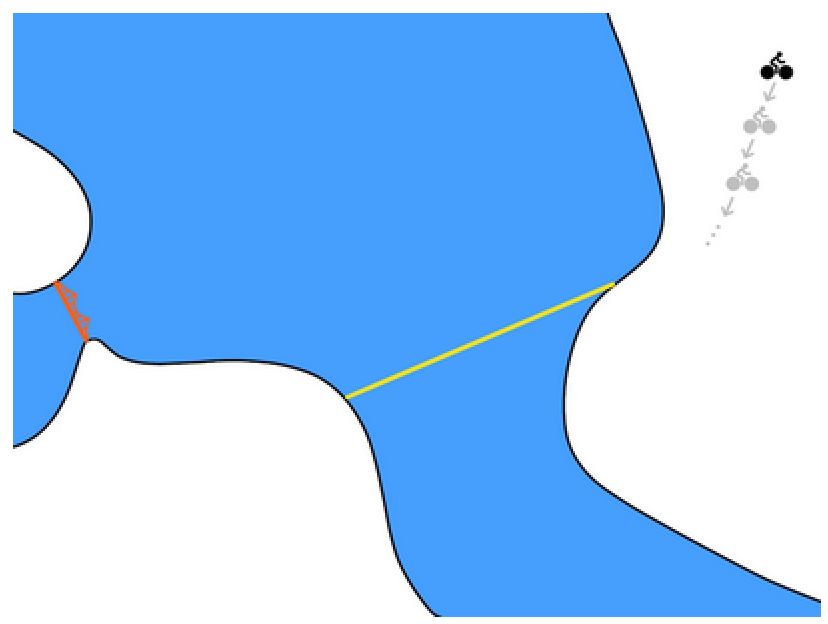
The concept of reality in the above chart is good but not realistic. The model-based method uses the model f(s,a) to predict the next state. The very short time for each step in the robot is very short. A more realistic plan will be a more intensive state transition like the following:
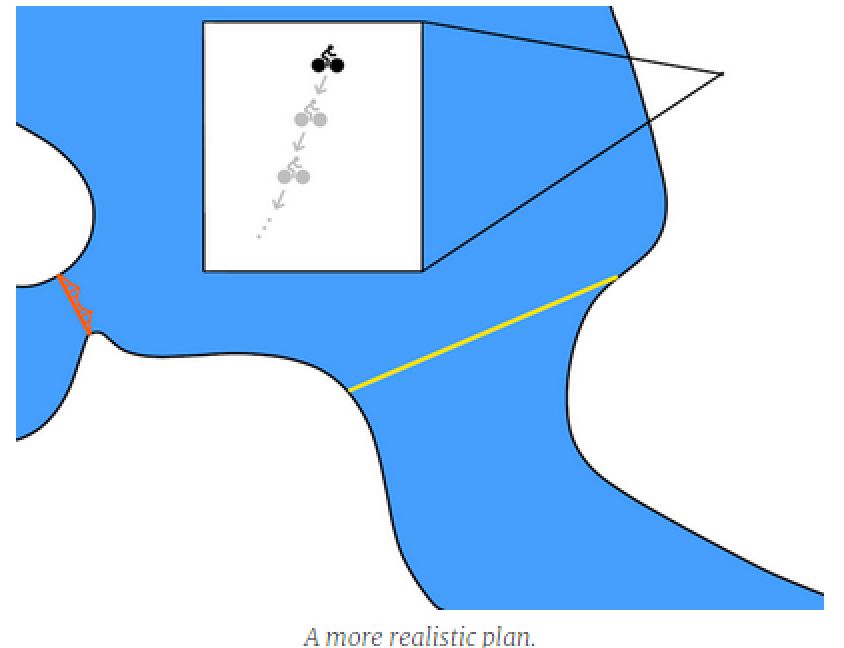
Recall that our planning of cycling every day is actually a very abstract process. We usually plan long-term goals rather than specific positions for each step. And we only carried out an abstract plan at the very beginning. As we just discussed, we need a starting point for trial and error learning, and we need to provide a mechanism to gradually increase the abstraction of the plan. So we introduced the time domain difference model.
Time domain difference model
The time-domain difference model is generally Q(s,a,sg,Ï„). Given the current state, behavior, and target state, the distance between the subject and the target is predicted when the Ï„ time step is long. Intuitively, TDM answers the question: "If I ride to the city center, how close will I be to the city center after 30 minutes?" For robots, the measured distance is mainly measured using Euclidean distance.
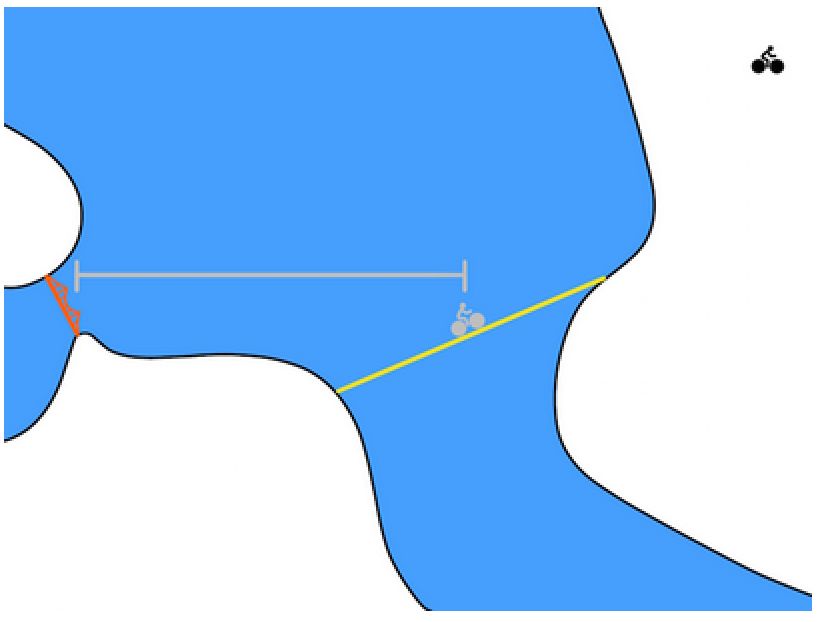
The gray line in the above figure represents the distance calculated by the TMD algorithm from the target. Then in reinforcement learning, we can think of TMD as a conditional Q function in a finite Markov decision process. TMD is a kind of Q function. We can use the modelless method to train. In general, people will use the deep confidence strategy gradient to train TDM and retrospectively mark the target and time to improve the sampling efficiency of the algorithm. Theoretically Q learning algorithms can be used to train TDM, but researchers found that the current algorithm is more effective. See the paper for more details.
Planning with TDM
After the training is over we can use the following objective function to plan:
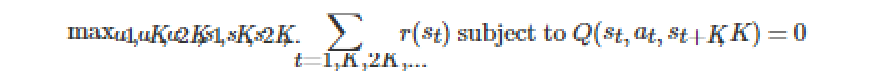
The difference from the model-based strategy here is that planning takes place every K steps, not every step. The zero at the right end of the equation guarantees the validity of each state transition trajectory:

The plan changes from the above-mentioned fine-grained steps to the overall, more abstract and long-term strategy of the following diagram:

When we increase K, we can get more long-term and abstract planning. Between the K-steps, a modelless method is used to select the behavior, a modelless strategy is used to abstract the process of achieving these goals, and finally the planning of the following diagram is implemented when K is large enough. The model-based method is used to select The abstract goal and no model approach is used to achieve these goals:
It should be noted that this method can only be optimized in the K-step, but in reality it only cares about some special states (such as the final state).
experiment
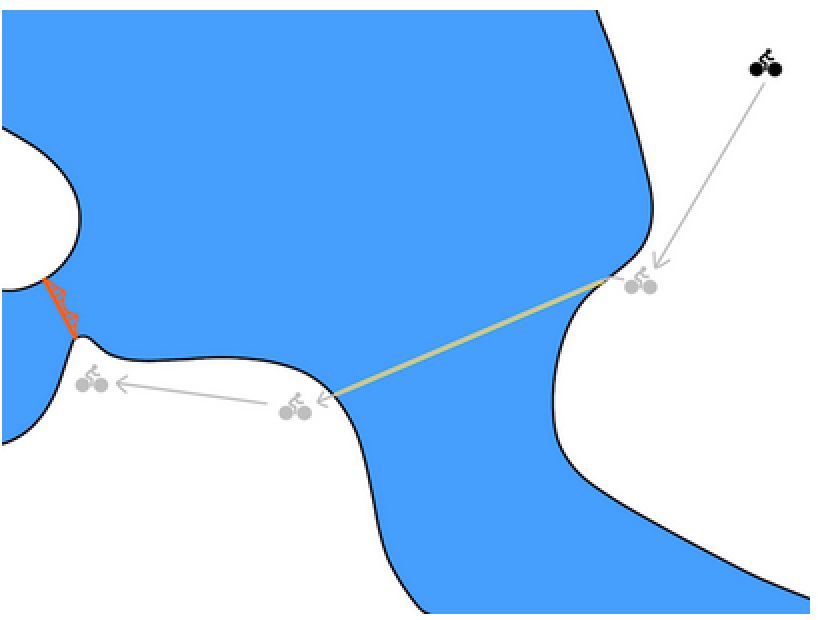
The researchers used the TMD algorithm to perform two experiments. The first is to use a simulated robotic arm to push the cylinder to the target position:
It can be found that the TMD algorithm is falling faster than the modelless DDPG algorithm and the model-based algorithm. Its fast learning ability comes from the previously mentioned model-based efficient sampling.
Another experiment is to use the robot to perform the task of positioning. The following figure shows the experimental schematic and learning curve:
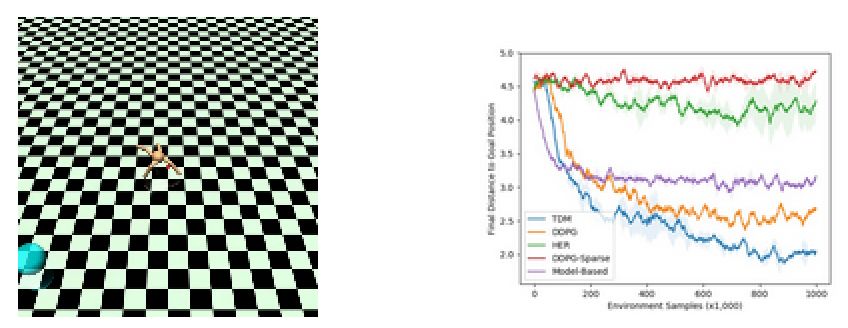
The model-based approach in the above figure has stagnated after training for a certain number of times, while the model-less method based on DDPG slows down, but the final effect is stronger than the model-based approach. The TMD method is fast and excellent, combining the advantages of the above two.
Future direction
The time-domain difference model provides an effective mathematical description and implementation method for modelless and model-based methods, but there is a series of work that needs to be refined. In the first theory, it is assumed that the environment and strategy are definite, but there is a certain degree of randomness in practice. This research will promote TMD's adaptability to the real environment. In addition TMD can be optimized with alternative model-based planning methods. Finally, it is hoped that the TMD will be used for the positioning and operation of real robots in the future, and even ride to the Golden Gate Bridge.
Industrial Zinc Alloy Die Casting
Industrial Zinc Alloy Die Casting,Alloy Electroplating Die Casting,Custom Metal Die Cast Buckle,Zinc Alloy Pressure Die Casting Parts
Dongguan Metalwork Technology Co., LTD. , https://www.diecast-pro.com